5.IRC算法

5.1 最陡下降法(Steepest descent)

最简单的获得IRC的方法就是固定步长的最陡下降法，由过渡态位置开始，每步沿着当前梯度方向行进一定距离直到反应物/产物位置，也称Euler法。由于最陡下降法及下文的IMK、GS等方法第一步需要梯度，而过渡态位置梯度为0，所以第一步移动的方向沿着虚频方向。最陡下降方法与IRC的本质相符，但是此法实际得到的路径是一条在真实IRC附近反复震荡的曲折路径，而非应有的平滑路径，对IRC描述不够精确。虽然可以通过更小的步长得以一定程度的解决，但是太花时间，对于复杂的反应机理，需要更多的点。也可以通过RK4(四阶Runga-Kutta)来走步，比上面的方法更稳定、准确，但每步要需要算四个梯度，比较费时。

5.2 IMK方法(Ishida-Morokuma-Kormornicki)

它是最陡下降法的改进，解决其震荡问题。首先计算起始点X(k)的梯度g(k)，获得辅助点X’(k+1)=X(k)-g(k)*s，其中s为可调参数。然后计算此点梯度g’(k+1)，在g(k)与-g’(k+1)方向的平分线上（红线所示）进行线搜索，所得能量最小点即为X(k+1)，之后再将X(k+1)作为上述步骤的X(k)重复进行。整个过程类似先做最陡下降法，然后做校正。此方法仍然需要相对较小的步长，获得较精确IRC所需计算的点数较多。 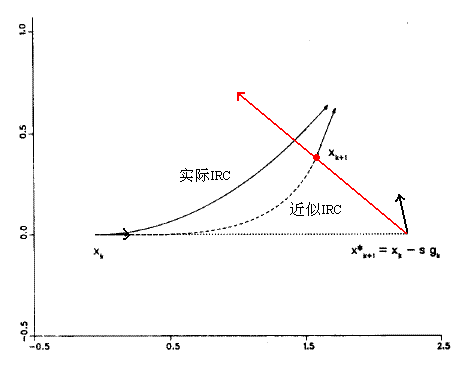img [图12]IMK方法示意图

Schmidt，Gordon，Dupuis改进了IMK的三个细节，使之更有效率、更稳定。(1)将X’(k+1)的确定方式改为了$X(k)-g(k)/ g(k) s$，即每一步在负梯度方向上行进固定的s距离，与梯度大小不再有关。(2)线搜索步只需在平分线上额外计算一个点的能量即可，这个点和X’(k+1)点的能量以及g’(k+1)在此平分线上的投影三个条件作联立方程即可解出曲线方程，减少了计算量。IMK原始方法则需要在平分线上额外计算两个点的能量与X’(k+1)的能量一起拟和曲线方程。(3)第一步在过渡态位置的移动距离Δq如此确定：ΔE=k(Δq^2)/2，k为虚频对应的力常数，ΔE为降低能量的期望值（一般为0.0005 hartree），这样可避免在虚频很大的鞍点处第一步位移使能量降低过多。

5.3 Müller-Brown方法

这是通过球形限制性优化找IRC的方法。首先将过渡态和能量极小点位置定义为P1和P2，由P1开始步进，当前步结构以Q(n)表示。每一步，在相距Q(n)为r距离的超球面上用simplex法优化获得能量极小点Q’（图中绿点），优化的起始点是Q(n-1)Q(n)与Q(n)P2方向的平分线b上距Q(n)为r距离的位置S（红点）。若Q(n)Q’与Q(n)P2的夹角较小，则Q’可当作是下一步位置Q(n+1)。如此反复，直到符合停止标准，比如下一步能量比当前更高（已走过头了）、与P2距离已很近（如小于1.2r）、或者与P2方向偏离太大（P1与P2点通过此法无法找到IRC）。最终所得到全部结构点依次相连即为近似的IRC，减小步长r值可使结果更贴近实际IRC。基于此方法也可以用于寻找过渡态，先将反应物和产物作为P1和P2，将二者距离的约2/3作为r，由其中一点在P1-P2连线上相距其r位置为初始位置进行球形优化得到O点，在O与P1、O与P2上也如此获得P1’与P2’，根据P1、P1’、O、P2’、P2的能量及之间距离信息以一定规则确定其中哪两个点作为下一步的P1和P2，确定新的P1和P2后重复上述步骤，直至P1与P2十分接近，即是过渡态。此方法计算IRC可以步长可设得稍大，第一步不需要费时的Hessian矩阵确定移动方向，缺点是获得的路径曲率容易有问题，对于曲率较大的反应路径需要减小步长。 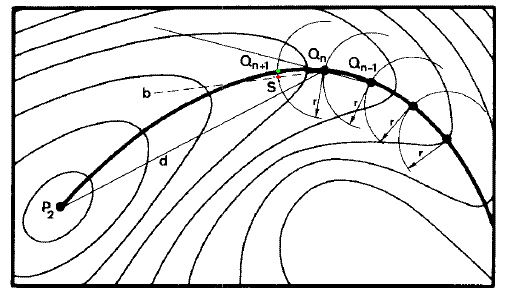img [图13]Müller-Brown方法示意图

5.4 GS(Gonzalez-Schlegel)方法

这是目前很常用，也是Gaussian使用的方法，见图14。首先计算起始点X(k)的梯度，沿其负方向行进s/2距离得到X’(k+1)点作为辅助点。在距X’(k+1)点距离为s/2的超球面上做限制性能量最小化，找到下一个点X(k+1)。因为这个点的负梯度（黑色箭头）在弧方向上分量为0，故垂直于弧，即其梯度方向在X’(k+1)到X(k+1)的直线上。这必然可以得到一段用于描述IRC的圆弧（虚线），它通过X(k)与X(K+1)点，且在此二点处圆弧的切线等于它们的梯度方向，这与IRC的特点一致，这段圆弧可以较好地（实线）。之后再将X(k+1)作为上述步骤的X(k)重复进行。

GS方法对IRC描述得比较精确，在研究反应过程等问题中，由于对中间体结构精度有要求，GS是很好的选择，而且用大步长可以得到与小步长相近的结果，优于IMK、Müller-Brown等方法。若只想得到与过渡态相连的反应物和产物结构，或者粗略验证预期的反应路径，对IRC精度要求不高，使用最陡下降法往往效率更高，尽管GS可以用更大步长，但每步更花时间。 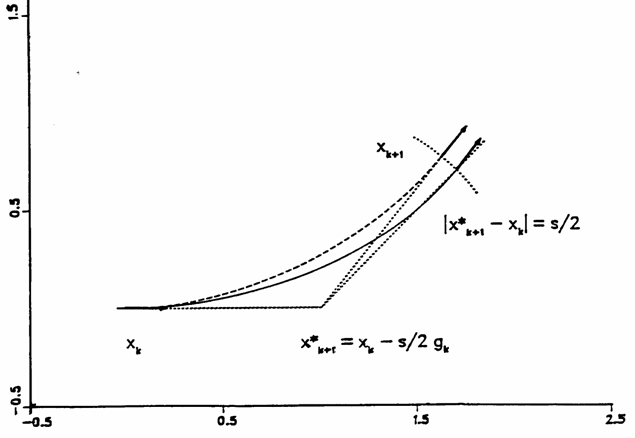img [图14]GS方法示意图

除上述外，IRC也可以通过已提及的EF、最缓上升法、球形优化等方法得到，它们的好处是不需要事先知道过渡态的结构。赝坐标法除了简单的反应以外，只能得到近似的IRC，由于结构的较小偏差会带来能量的较大变化，容易引入滞后效应，所以这样得到的势能曲线难以说明问题。